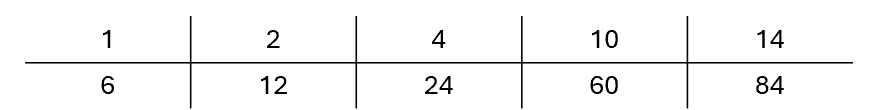Building Stronger Mathematical Thinkers Through Progressive Formalization
This research overview highlights the role of progressive formalization in helping students build stronger reasoning skills, retain concepts longer, and apply their knowledge in new situations.
Introduction:
Progressive formalization is the gradual movement from informal problem-solving toward formal mathematical reasoning. Rather than starting with abstract algorithms, it builds from students’ intuitive strategies and everyday experiences, then progresses through visual models and semi-formal methods before reaching symbolic representations. This pathway reflects research in math education and cognitive science, supporting deeper ownership, long-term retention, and transfer (Sweller, 1988).
What is Progressive Formalization?
Progressive formalization is an instructional approach in which mathematical ideas are introduced and developed through a sequence that moves students from concrete, intuitive methods to abstract, standardized mathematical forms. In this approach, mathematical concepts are not presented as detached rules but are built meaningfully on students’ existing knowledge and experiences. Key theorists, such as Hans Freudenthal, who developed Realistic Mathematics Education (RME), and Jerome Bruner, whose theory describes the movement from enactive (action-based) to iconic (visual) to symbolic (abstract) representations, have both described this natural progression.
The journey of progressive formalization commonly unfolds through several stages. To illustrate, consider how multiplication can be taught: learners might begin by modeling a real situation (such as organizing apples into baskets) with objects or pictures. Next, students might explore the total quantity through skip counting, which provides early abstraction beyond one-to-one correspondence. As comfort grows, teachers introduce structured visual representations, such as arrays or area models, connecting multiplication to geometric and repeated addition concepts. Semi-formal methods follow, such as using partial products (decomposing numbers into more manageable chunks, like 10 and 4 in 14 × 6) or ratio tables that track quantities through patterns and scaling. Eventually, the formal multiplication algorithm is introduced, with students recognizing it as a summary of the patterns, ideas, and strategies they have already explored in depth.
The Stages of Progressive Formalization: A Multiplication Example
To demonstrate progressive formalization in concrete terms, let us follow a typical trajectory for multiplication learning in an elementary mathematics classroom:
Stage 1: Real-Life Contexts and Manipulatives
The process begins with a story or situation from everyday life. For instance, a teacher might ask, “If there are 4 baskets, and each basket has 6 apples, how many apples are there in all?” Students model this with physical counters or chips, building four groups of six. This viscerally links multiplication to the tangible world, encouraging sense-making and anchoring early learning in meaningful contexts.
Stage 2: Skip Counting
Once students are comfortable with the idea of equal groups, the teacher prompts them to count in steps: 6, 12, 18, 24. This step shifts thinking from one-to-one or additive reasoning to a pattern-based understanding of repeated addition. Students begin to recognize the multiplicative structure underlying the problem and become comfortable extending the count beyond what manipulatives can easily represent.
Stage 3: Area Model and Arrays
After working with groups, students are encouraged to organize their thinking into arrays or area models. On paper or with tiles, 4 rows of 6 apples become a rectangle divided into 24 units. This visual structure reinforces the idea that multiplication involves both grouping and arrangement, and supports connections to geometry and the distributive property. It also enables students to “see” the total without counting one by one. Area models become especially powerful as students face more complex multiplication, such as multiplying two-digit numbers by breaking them into tens and ones, and representing each part visually.
Stage 4: Partial Products
As numbers become larger, students move from modeling every object to decomposing numbers into manageable chunks. With 14 × 6, for example, students use partial products: they break 14 into 10 and 4, multiply 10 × 6 and 4 × 6, and then add the results (60 + 24 = 84). Partial products can be represented by expanded area models or tables, providing a bridge from visual representation to symbolic manipulation. This stage concretely illustrates the distributive property and lays the groundwork for mental flexibility.
Stage 5: Ratio Table
Semi-formal representations, such as the ratio table, further bridge the gap between enactive and symbolic understanding. A ratio table for 14 × 6 might look like this:
Using such a table, students notice and use multiplicative patterns, practice scaling, and organize their computations efficiently.
Stage 6: Formal Algorithm
Only after these steps do students encounter the standard (vertical) multiplication algorithm. Because they have experienced the reasoning behind each part of the calculation, the algorithm is not arbitrary—they understand, for example, why multiplying the ones and tens separately and then combining the results makes sense. They view the algorithm as a powerful summary or shortcut for what they have already completed concretely and visually.
Why is Progressive Formalization Effective?
Progressive formalization leads to deeper conceptual understanding because ideas are developed across contexts before they are formalized. Students see strategies as logical extensions of their own reasoning rather than as arbitrary procedures. This process builds strong mental schemas, making new knowledge more meaningful, memorable, and connected to prior experiences (Bruner, 1966).
The approach also fosters flexibility and problem-solving skills. Working with mathematics in physical, visual, and symbolic forms helps learners switch strategies, see relationships, and adapt to new or non-routine problems. Such adaptability supports both creativity and practical success.
From a cognitive perspective, gradual movement from concrete to abstract helps manage cognitive load. By grounding new learning in familiar, hands-on, and visual experiences, teachers reduce overwhelm and anxiety while building student confidence (Sweller, 1988).
Progressive formalization strengthens retention and transfer. Revisiting concepts through manipulatives, diagrams, and symbols creates multiple memory connections that act as retrieval cues. Research shows this layered approach leads to longer-lasting understanding and higher achievement (Freudenthal, 1991; van den Heuvel-Panhuizen & Drijvers, 2014).
Finally, the approach provides social and emotional benefits. Early success with intuitive strategies reduces math anxiety, nurtures positive attitudes, and encourages classroom cultures that value reasoning, exploration, and equitable participation.
Cognitive and Psychological Mechanisms
Progressive formalization aligns closely with principles of cognitive psychology and learning theory. Cognitive load theory suggests that beginners cannot process large amounts of unfamiliar information simultaneously (Sweller, 1988). By starting with concrete situations and gradually increasing abstraction, students build comfort and understanding at each stage before advancing to more complex concepts.
The process supports schema development and memory. Working with manipulatives, visuals, and semi-formal methods enables learners to create mental models that are linked to real-world experiences. When formal algorithms are finally introduced, students view them as coherent summaries of what they already know, which strengthens both immediate comprehension and long-term retention.
Scaffolding within the zone of proximal development provides further support for growth and development. Teachers provide prompts, questions, and models that are gradually removed as students gain independence with abstract ideas. Additionally, because concepts are experienced through multiple modalities—acting, seeing, saying, and writing progressive formalization naturally promotes stronger, more durable memories.
Disadvantages and Challenges
Progressive formalization requires a significant amount of time and expertise. Teachers must allow space for multiple representations, discussion, and depth, which can be difficult in schools constrained by pacing guides or testing schedules. In addition, the approach demands strong pedagogical knowledge: teachers must both recognize students’ informal strategies and know how to connect them to formal mathematics.
The approach can also face misalignment with expectations and assessments. If transitions to formal methods are not explicit, students may remain stuck in informal strategies. Some observers may misinterpret the gradual approach as “delaying real math,” especially since standardized tests often reward procedural fluency over conceptual understanding. Without professional support and assessment structures that value reasoning, the benefits of progressive formalization may be overlooked.
Implications for Curriculum and Teaching Practice
To maximize impact, classrooms must deliberately sequence learning from concrete to visual to abstract. Tasks should be open and rooted in authentic contexts, with time set aside for students to explore, discuss, and refine their reasoning. Crucially, transitions between representations must be explicit so students see how informal ideas connect to more formal mathematics.
Teacher learning and assessment also play vital roles. Professional development should emphasize both mathematical content knowledge and children’s developmental progressions, equipping educators to value informal strategies, guide dialogue, and link multiple approaches to formal methods. Likewise, assessments must go beyond correct answers to capture students’ conceptual understanding, reasoning flexibility, and ability to shift between representations.
Conclusion
Progressive formalization is a research-supported approach that prioritizes student sense-making, engagement, and conceptual depth. By moving learners from informal, experience-based strategies through visual and semi-formal representations to abstract algorithms, teachers align instruction with how people naturally acquire knowledge. This process strengthens understanding, boosts retention, and fosters confidence, creativity, and a more positive disposition toward mathematics. Progressive formalization supports flexible problem-solving, durable memory, and broader access to powerful ideas. Most importantly, it helps students see mathematics not as arbitrary procedures but as a connected, meaningful discipline they can own, understand, and apply throughout their lives.
References
Bruner, J. S. (1966). Toward a theory of instruction. Harvard University Press.
Freudenthal, H. (1991). Revisiting mathematics education: China lectures. Kluwer Academic Publishers.
Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257–285. https://doi.org/10.1207/s15516709cog1202_4
van den Heuvel-Panhuizen, M., & Drijvers, P. (2014). Realistic Mathematics Education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 521–525). Springer. https://doi.org/10.1007/978-94-007-4978-8_170
Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Harvard University Press.
Social Media
Are We Rushing Students Into Formal Math Too Soon?
When students struggle, the tendency is often to push them straight into rules and procedures. However, research shows that skipping the concrete-to-visual-to-abstract progression can leave learners confused, anxious, and disconnected from the mathematical concepts themselves.
Progressive formalization offers another way. By starting with intuitive strategies and models before moving on to formal algorithms, students develop a deeper understanding, retain concepts for longer, and acquire flexible problem-solving skills.
In this research overview, you’ll discover:
Why memorization-first approaches rarely lead to lasting knowledge
How progressive formalization supports cognitive load, memory, and motivation
Practical examples showing how multiplication develops step by step
The challenges—time, training, and assessment—that teachers and leaders need to consider
Let’s reframe math instruction not as a race to procedures, but as a structured journey where students own and understand the mathematics they learn.
Read the complete research overview to see how progressive formalization can change the way we teach—and how students learn