Are your students Truly Understanding Line Plots? Research-based strategies to close gaps
This research overview highlights the strategies teachers can employ to help students have a better understanding of Line Plots.
Introduction:
Line plots are a gateway to data literacy—but many students misinterpret them despite repeated instruction. Research shows that even after lessons, students often confuse quantities with counts, misread empty categories, or struggle to connect symbols to real-world data (NCTM, 2014). These gaps hinder critical thinking and future work with graphs. This overview synthesizes current research on these misconceptions, connects them to evidence-based teaching practices, and offers practical recommendations to help educators build students’ data literacy skills.
Common Misconceptions About Line Plots
What are the most common misconceptions students display when interpreting or constructing line plots?
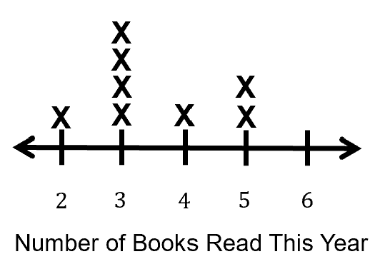
Research consistently reveals several key misconceptions students hold regarding line plots. A recurring error is confusion about what is being counted—students often mix up the number of different quantities (the numbers on the line plot, like "2 books" or "3 books") with the actual number of students represented (that is, the total number of Xs above all quantities). For example, consider this typical line plot representing the number of books read by students this year. In this example, a student might look at this line plot and say, “There are five students,” or “There are five books read,” simply because there are five different quantities shown on the axis (2, 3, 4, 5, and 6). The actual total number of students is found by counting all of the Xs: 1 + 4 + 1 + 2 = 8 students.
Other students may misinterpret what each X represents. It is common for students to think “each X is a book,” confusing the data point for the item measured, while other students think an X stands for more than one student or book (e.g., “Each X is worth two students”). In both cases, it is important to clarify: each X stands for one individual student's response, unless the key says otherwise. When a student says, “Each X stands for two [students],” a teacher might respond, “Let’s count together—how many Xs do you see for 3 books? How many students are there?”
Students also struggle with reasoning about the range or the maximum value shown by the data. For instance, a student may look at “3 books,” which has the most Xs, and mistakenly claim that “3 is the most number of books read,” when in fact the largest value shown on the axis is “6 books.” The actual maximum possible (largest value represented) is 6 books, though no students read that many. In this example, no X appears above “6 books,” meaning zero students read that many, but the range extends to include that value. Other students may see empty slots such as above “6 books” and believe this means data is missing, rather than understanding that these represent zero students.
Finally, the omission or incorrect labeling of axes and units frequently obscures the data’s context and contributes to misinterpretations (NCTM, 2014; Friel et al., 2001). For instance, if the line plot is not labeled with what is counted (e.g., ‘Number of Books’) or whether each X represents a student or a book, students may misinterpret the meaning of the data.
Important clarification: The term “categories” is frequently used in bar graphs, which show categorical data such as favorite fruit. For line plots, however, we teach that the numbers on the axis represent quantities—measurable, numeric values (such as the number of books read, or length in inches). This distinction should be made clear to both teachers and students to avoid confusion between categorical and quantitative data.
When creating classroom activities, ensure that the data displayed in line plots are quantitative. For example, rather than plotting “favorite fruits,” which is categorical and best for bar graphs, use measurements such as ‘number of pieces of fruit eaten in one day’ for a line plot.
Origins and Persistence of Misconceptions
Why do these misconceptions persist despite instruction?
Several interrelated factors contribute to the persistent misconceptions students hold about line plots. Chief among them is the incorrect transfer of procedures and ideas from other visual data displays, like bar graphs, to line plots. For example, students often look for the “tallest bar” (here, the quantity with the most Xs—like “3 books” in the revised example), wrongly assuming that this visually highest group represents the largest value in the data set, as they would with categorical bar graphs. This incorrect transfer of procedures and confusion between categorical and quantitative thinking lead to persistent errors in interpreting line plots (Lehrer & Schauble, 2004; Friel et al., 2001).
Additionally, many students possess incomplete or inaccurate mental models of how line plots represent data, making it difficult to develop a robust understanding (Hattie, 2011). For example, students may not realize that a blank space above “6 books” means zero students—no one in the class read six books—not that data for six books is missing. Without explicit opportunities to discuss and clarify their thinking—and without targeted teacher intervention—these false assumptions go uncorrected and persist over time
Instructional Strategies to Address Misconceptions
What instructional strategies are most effective in addressing line plot misconceptions?
Addressing misconceptions about line plots requires a multi-faceted and intentional instructional approach. Teachers should begin by using precise mathematical language and clear visual models to clarify the meaning of each symbol. It is essential to emphasize that each X on a line plot represents a single student’s response (the data point), not the item being measured or more than one data point (NCTM, 2014; Friel et al., 2001). When presenting a line plot, teachers can prompt students to count the Xs, explicitly label what each X represents, and model how to determine total counts—reinforcing the connection between the graphical marks and the underlying data.
Building conceptual understanding is most effective when instruction follows Bruner’s stages of representation—enactive, iconic, and symbolic. Teachers can start by lining up actual objects (like pencil boxes or cubes) that represent each data point. Next, students can create mathematical pictures or diagrams of these items (iconic stage) before transitioning to representing the data as Xs on a line plot (symbolic stage). Engaging students in hands-on activities that involve collecting and plotting measurable, quantitative data—such as counting the number of pages read or the number of different colors in a handful of beads—makes the process meaningful and concrete (Lehrer & Schauble, 2004; Fuson & Murata, 2007). In contrast, plotting categorical data (like favorite fruits) is more appropriate for bar graphs.
Finally, explicit attention to labeling is vital for accuracy and interpretation. Teachers should consistently label axes, units of measurement (not categories), and include a key if needed, so students clearly understand what each X represents. This staged and explicit instructional approach is further strengthened through ongoing diagnostic assessment—posing questions and analyzing student work to surface misconceptions—and by providing immediate, targeted feedback that addresses both correctness and the underlying reasoning (Jacobs, Lamb, & Philipp, 2010; Black & Wiliam, 1998; Hattie & Timperley, 2007; Heritage, 2010). In this way, misunderstandings are addressed early, supporting students in developing a robust and transferable understanding of line plot concepts.
Diagnostic Assessment and Targeted Feedback
How can teachers ensure that misconceptions are identified and addressed promptly?
To ensure misconceptions are addressed promptly, teachers should employ a robust assessment strategy. Diagnostic assessments, such as asking students to explain their reasoning or identify errors in sample line plots, make student thinking explicit, allowing for timely and targeted interventions tailored to individual needs (Black & Wiliam, 1998; Jacobs et al., 2010). For example, present students with the books-read line plot and ask: “How many students read 5 books? How many read 6 books?” This reveals whether students understand the correspondence between Xs and frequency, and whether they correctly interpret empty categories. Formative assessment, or ongoing checks for understanding, enables teachers to adjust their instruction in response to student learning, supporting deeper understanding (Heritage, 2010). Moreover, immediate and specific feedback is crucial for correcting misunderstandings. This feedback should address not only the correctness of student responses but also the underlying reasoning processes, guiding students toward more accurate and flexible understandings of line plot concepts (Hattie & Timperley, 2007).
Progression of Representations
Teaching line plots effectively requires a progression through Bruner’s representational stages: enactive (using manipulatives), iconic (using pictorial representations), and symbolic. While all stages are important, the transition from iconic to symbolic representations is particularly critical. Students require many opportunities to connect the visual representations of the iconic stage with the abstract notations of the symbolic stage before achieving a true understanding (Fuson & Murata, 2007; NCTM, 2014; Lesh, Post, & Behr, 1987). This deliberate progression fosters deep and transferable understanding, aligning with established research in mathematics education.
Parallels with Broader Mathematics Education Research
How do these findings align with broader research on effective mathematics teaching?
Students’ struggles with line plots underscore the importance of aligning instructional practices with cognitive principles. Research emphasizes the importance of precise language, explicit modeling, and opportunities for students to articulate their reasoning (NCTM, 2014). A successful approach uses Bruner’s representational stages—enactive, iconic, and symbolic—carefully sequencing instruction to facilitate a smooth transition between concrete experiences, visual representations, and abstract notation. This approach prioritizes conceptual understanding, embeds tasks within meaningful contexts, and promotes data literacy for all learners (Fuson & Murata, 2007; NCTM, 2014). Returning to the earlier example throughout instruction and assessment helps anchor these concepts in reality and supports retention.
Conclusion
Data literacy and strong mathematical reasoning hinge on overcoming common misconceptions about line plots. Teachers can effectively achieve this by employing research-based strategies, such as explicit language, visual models, and diagnostic assessments, while using real classroom scenarios and feedback to make learning stick. By equipping students with accurate and flexible understandings of line plots, educators set them up for success in more advanced data analysis.
References
Black, P., & Wiliam, D (1998). Assessment and classroom learning. Assessment in Education: Principles, Policy & Practice, 5(1), 7–74.
Friel, S. N., Curcio, F. R., & Bright, G. W (2001). Making sense of graphs: Critical factors influencing comprehension and instructional implications. Journal for Research in Mathematics Education, 32(2), 124–158.
Fuson, K. C., & Murata, A (2007). Integrating NRC principles and the NCTM process standards to form a class learning path model for teaching the Common Core. Journal for Research in Mathematics Education, 38(3), 257–285.
Hattie, J (2011). Visible learning for teachers: Maximizing impact on learning. Routledge.
Hattie, J., & Timperley, H (2007). The power of feedback. Review of Educational Research, 77(1), 81–112.
Heritage, M (2010). Formative assessment: Making it happen in the classroom. Corwin.
Jacobs, V. R., Lamb, L. L. C., & Philipp, R. A (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education, 41(2), 169–202.
Lesh, R., Post, T., & Behr, M (1987). Representations and translations among representations in mathematics learning and problem solving. In C. Janvier (Ed.), Problems of representation in the teaching and learning of mathematics (pp. 33–40). Lawrence Erlbaum Associates.
National Council of Teachers of Mathematics (2014). Principles to actions: Ensuring mathematical success for all.
Shaughnessy, J. M (2007). Research on statistics learning and reasoning. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 957–1009). Information Age.
Watson, J. M., & Callingham, R. (2003). Statistical literacy: A complex hierarchical construct. Statistics Education Research Journal, 2(2), 3–46.
Social Media
How confident are your students in interpreting line plots, and are you sure they are “reading” the data as intended?
Building data literacy starts early, and understanding line plots is a foundational skill in elementary mathematics. Yet, research shows persistent student misconceptions—such as misinterpreting what each “X” represents, confusing quantities with frequencies, or misreading empty categories.
Why do these misconceptions persist? Often, students apply strategies from bar graphs (categorical data) to line plots (quantitative data), or they lack clear mental models for interpreting visual data.
What can educators do?
Use precise mathematical language and clear models to clarify meanings.
Progress through Bruner’s stages: hands-on manipulatives (enactive), pictures (iconic), then abstract Xs (symbolic).
Provide regular opportunities for students to explain their thinking and address misconceptions through diagnostic assessment and targeted feedback.
Always label axes and units clearly, connecting each step back to real-world and classroom data.
Helping students overcome these hurdles is not just about correct answers—it’s about building flexible, robust data reasoning. As research and classroom experience demonstrate, explicit strategies, visual models, and formative feedback make all the difference.
Let’s empower students to become confident data interpreters—one line plot at a time!
Please read the complete research overview to learn how we can make reteaching work for all students.